How to Use Excel PMT Function

The PMT Formula in Excel is used to calculate the periodic payment amount for a loan or an investment, taking into account interest rates, the number of payment periods, and the present value or future value of the loan or investment

PMT full form in Excel is "Payment", indicating the recurring money transfer, like monthly installments or interest payments.

1. Syntax of the PMT Function

The PMT formula has the following syntax:

=PMT(rate, nper, pv, [fv], [type])

rate: The interest rate for each period.

nper: The number of payment periods.

pv: The present value or the principal amount.

[fv] (optional): The future value or a cash balance you want to attain after the last payment.

[type] (optional): Indicates whether payments are made at the beginning or end of each period. Use 0 for end-of-period payments (default) and 1 for beginning-of-period payments.

2. PMT Function Examples

The PMT function in Excel serves multiple purposes, from calculating loan payments to forecasting savings or investment contributions.

2.1 Calculating Monthly Loan Payments

Suppose you want to calculate the monthly payment for a loan of $20,000 with an annual interest rate of 5% for 5 years (60 months).

=PMT(5%/12, 5*12, -20000)

Here's how the formula works:

1. The annual interest rate of 5% is divided by 12 to get the monthly interest rate (5%/12).

2. The number of payment periods is 5 years (60 months), so we use 5*12.

3. The present value (loan amount) is -$20,000 (negative because it's an outgoing payment).

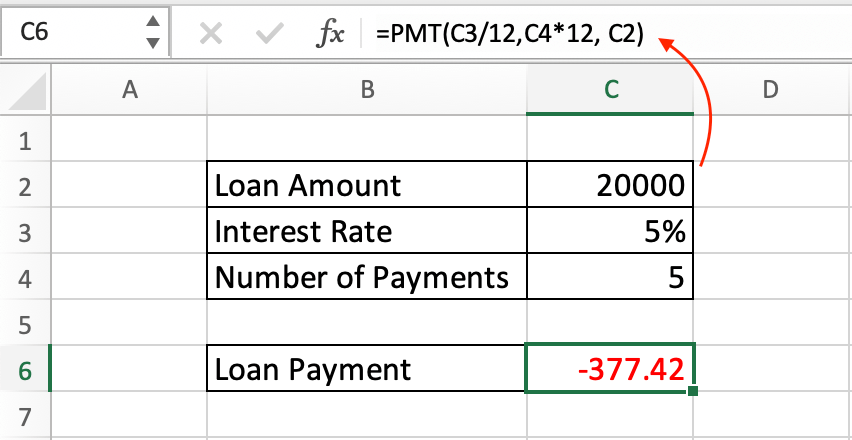
The result is approximately -$377.42.

This means you would need to make monthly payments of approximately $377.42 to pay off a $20,000 loan with a 5% annual interest rate over 5 years.

The negative sign indicates that it's an outgoing payment.

2.2 PMT Calculation for Investments

You can also use the PMT formula to determine how much you need to save or invest each month to reach a specific future value.

For example, if you want to have $50,000 in 10 years with an annual interest rate of 7%:

=PMT(7%/12, 10*12, 0, 50000)

Here's how the formula works:

1. The annual interest rate of 7% is divided by 12 to get the monthly interest rate (7%/12).

2. The number of payment periods is 10 years, which is equivalent to 120 months (10*12).

3. The present value (PV) is 0 because you don't have any money saved or invested initially.

4. The future value (FV) is $50,000.

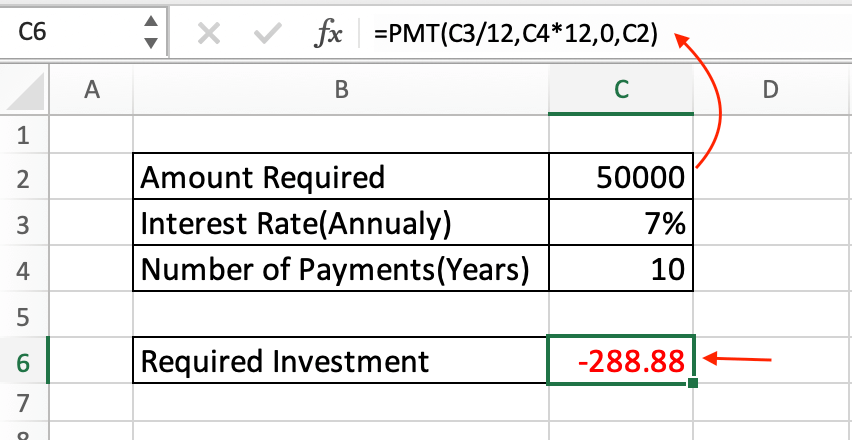
The result is approximately -$288.88.

This means you would need to save or invest approximately $288.88 per month for 10 years at a 7% annual interest rate to accumulate $50,000.

The negative sign indicates that it's an outgoing payment or contribution.

2.3. PMT Function Formula for Quarterly Calculation

If your interest rate is compounded quarterly or semi-annually, you need to adjust the formula accordingly by dividing the annual rate and multiplying the number of periods.

Let's say you want to calculate the monthly contribution needed to reach a future value of $50,000 in 10 years with an annual interest rate of 7% compounded quarterly.

Here's how you would adjust the PMT formula:

=PMT((7%/4), 10*4, 0, 50000)

Here's how the formula works:

1. The annual interest rate of 7% is divided by 4 to get the quarterly interest rate (7%/4).

2. The number of payment periods is 10 years, which is equivalent to 40 quarter (10*4).

3. The present value (PV) is 0 because you don't have any money saved or invested initially.

4. The future value (FV) is $50,000.

The correct result is approximately -$873.60.

So, with quarterly compounding, you would need to save or invest approximately $873.60 per month for 10 years at a 7% annual interest rate to accumulate $50,000.

The negative sign indicates that it's an outgoing payment or contribution.